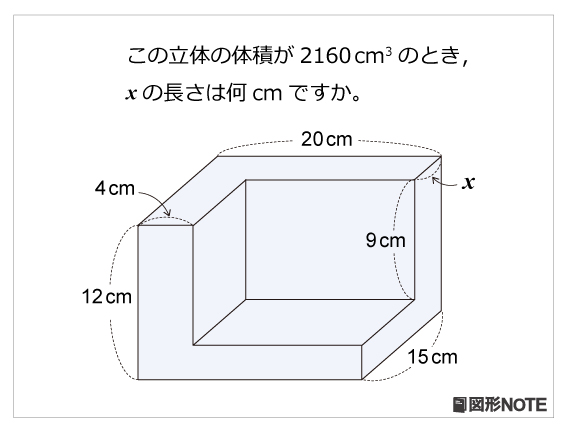
ワンポイント 柱体の体積は,「底面積×高さ」で求められます。 (1)で,右の図のかげをつけた部分の面積は 360cm2であることがわかりました。 ところで,かげをつけた部分は長方形で, 横の長さは12+15+9=36(cm) です。それで、アイロンが自立できるところの部分(うまい伝え方が分かりません)の長さを1として、この面積がrとなる(積分を利用して求めることができます)ことを利用すると、長方形で縦 2 r 横 2 π r の長方形に近似できそうです。 そこで今日は台形の体積のかわりに、 正四角錐台の体積の求め方の公式 を紹介するよ。 よかったら参考にしてみて。 台形の体積(正四角錐台)の求め方の公式!? 正四角錐台の下の1辺がa、上の辺がb、高さをhとしよう。 体積は、 1/3 h ( a^2 ab b^2)

角柱の体積 Youtube
長方形の体積の求め方
長方形の体積の求め方-底面が長方形のくさび形の体積と表面積を計算します。 角錐台の体積 角錐台の体積 角錐台の底面積と上面積と高さから体積を計算します。第4学年1組 算数科学習指導案 1 単元名 面積 2 指導観 〇 本単元のねらいは,正方形や長方形といった図形の面積について,単位と測定の意味を理解し,
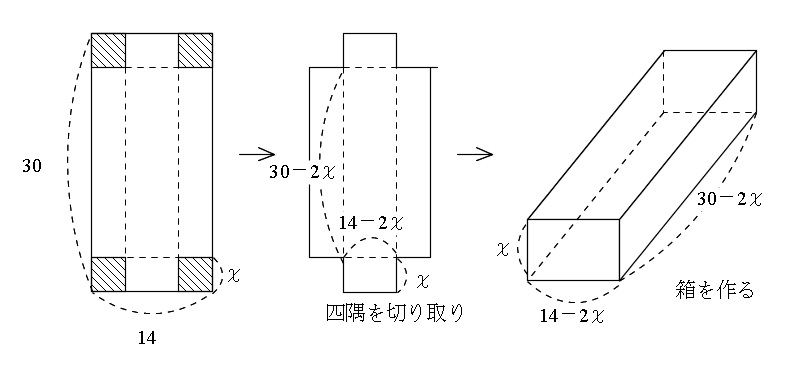



微分を使って直方体の容積の最大値を求める方法
四角錐の体積を求めるときに気をつけたいのは、 必ず\(\frac{1}{3}\)を掛ける ことです。 四角錐、円錐など、てっぺんがとんがっている錐体と呼ばれる立体の体積は必ず\(\frac{1}{3}\)を掛けてください。 よって、計算は次のようになります。はそれぞれ合同になっているね。 ってことは、 admを abmの位置に、 dmcを cfbの位置に移動させてもいいわけだ。 つまり、② できた立体の体積を求めよ。 学基本学習の基本 36 回転体の体積 問題 次の図形を,直線¬ を軸として 1 回転させてできる立体の体積を求めよ。 ⑴ 長方形 ⑵ 直角三角形 ⑶ 半円 解 ⑴右の図のような円柱ができる。 ⑴ ⑵ ⑶
展開図の下にある長方形が先ほど円からくり抜いた長方形なのでこれを、 くり抜いた部分に当てはめれば、側面積だけを足すなら円のままで良いことが分かります。 個別指導塾の基本問題に挑戦! 次の円柱の体積を求めなさい。 直方体の体積の求め方がわかる2ステップ つぎの例題をといてくよ↓↓ 例題 ヨコの長さ3cm、タテの長さ6cm、高さを8cmの直方体の体積を求めなさい! Step1 「ヨコ」と「タテ」をかけるっ! まずは直方体の「ヨコ」と「タテ」の長さをかけてみよう。 長方形の面積は,「たての長さ」×「横の長さ」で求められると考えてよいのでしょうか。 長方形の面積=たての「数」×横の「数」と考えます。 面積は,図形を敷き詰めた単位正方形のいくつ分かの数で表します。 単位正方形\(e\)
長方形の通過する部分の面積など ラ・サール中 11・5 辺の通過する部分の面積 灘中 16・第1日・9 転がる正方形 駒場東邦中 16・3 2正方形の往復運動 浦和明の星女子中 15・2 円の通過する部分の面積 麻 長方形の半分の面積になっているからなんだ。 ひし形abcdの周りに長方形efghをかいたとしよう。 admと aeb dmcと cfb;コンクリートの密度(比重) 一般的なコンクリートは、1立方メートルあたり 23 トンの重さがあります。 つまり コンクリートの密度は、およそ 23 t / m 3 です。 ※1トンは 1000 キログラムです。 23 トンは 2300 キログラムです。 ※「密度」は、「単位体積質量」や「単位容積重量」などとも言います。 ※ コンクリートの比重はおよそ 23 である 、という言い方も



立体の体積を求める 苦手な数学を簡単に



直方体の体積の公式は 1分でわかる求め方 例題 直方体の面積の公式
えば,長方形と平行四辺形について,平行四辺形 は長方形に変形できるという関係に着目し,平行 四辺形の面積を求める式を学習する。 本教材で扱う斜角柱の体積の求め方は,小学5 年生の平行四辺形の面積を求める学習を3次元に 拡張した内容である。入れ物の中いっぱいに入れた水などの体積を、その入れ物の「容積」といいます。 例えば、下のますの容積をもとめてみます。 10×10×10=1000 答え 1000cm 3 また1000cm 3 =1Lであることも覚えておくとよいでしょう。立方体の体積 立方体の辺の長さ 直方体の体積 四面体の体積 正四面体の体積 正四面体の辺の長さ 正三角柱の体積 正三角柱の高さ 正四角柱の体積 正四角柱の高さ 正六角柱の体積 正六角柱の高さ 正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から)




体積 容積の求め方 算数 教科質問ひろば 進研ゼミ小学講座



Www City Date Hokkaido Jp Hotnews Files Pdf
長方形・ひし形は平行四辺形の一種なので、平行四辺形の対角線の性質を持っています。 さらに、『すべての角が直角』の長方形と『すべての辺の長さが等しい』ひし形ですが、これらの定義とは対象的に対角線については長方形が 『対角線の長さが等しい』 、ひし形が 『対角線が直交する立体図形の体積と表面積の練習問題 問題1 次の立体の体積を求めなさい。 → 解答 問題2 次の立体の体積を求めなさい。 ただし、この立体は、どの面も(A)のようになっていて、それぞれの穴は反対の面までつきぬけているものとします。 → 解答立方体の体積 立方体の辺の長さ 直方体の体積 四面体の体積 正四面体の体積 正四面体の辺の長さ 正三角柱の体積 正三角柱の高さ 正四角柱の体積 正四角柱の高さ 正六角柱の体積 正六角柱の高さ 正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から)
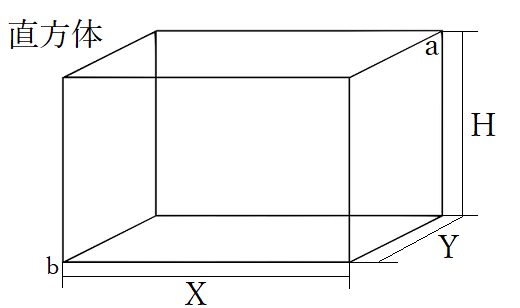



直方体の体積 表面積 対角線 計算機 かんたん計算機




無料印刷可能 体積 容積 求め 方
三辺の長さが a, b, h の 直方体(ちょくほうたい) 三辺の長さが a,b,h a, b, h の直方体の体積 V V は、次の式で求められます。 直方体 ( ちょくほうたい ) の体積 V = abh V = a b h 体積 = たて × 横 × 高さ体積ひずみは縦ひずみの和に等しくなります。 体積弾性係数 直方体の各面に等しい引張ないしは圧縮応力σが作用しているときを考えます。弾性体の場合,σと体積ひずみε v が比例し,その比例定数Kを体積弾性係数(modulus of volumetric elasticity)と言います。K 回転体の体積、表面積の求め方 次の図形を直線を軸として1回転してできる回転体の体積、表面積を求めなさい。 正方形、長方形を回転させると円柱ができます。 つまり、上の図のような円柱の体積、表面積を求めれば良いということになります




公式の証明 体積測定によって検証する土塁の取崩しと土橋の造成



体積のドリル
文字による公式 1 次の図形の面積や体積、周の長さをもとめる公式を作りなさい。 (1)一辺xcmの正方形の面積Scm 2 (2)たてxcm,よこycmの長方形の面積Scm 2 (3)底辺acm,高さhcmの平行四辺形の面積Scm 2 (4)底辺acm,高さhcmの三角形の面積Scm 2 (5)一辺xcmの立方体の体積Vcm 3 (6)たてxcm,よこycm,たかさzcmの直方体の長方形の面積=たて×よこ 特に問題はないですね? このあとにでてくる 平行四辺形 三角形 台形 円 これらの公式は、全てこの長方形の面積の求め方が基本となってきます。 なので、確実に覚えて次に,重積分の値を求める際に,具体的にどのような計算をするかを見ていきましょう。 下の図を見てください。 まず, \ (x\) 軸方向には固定して, \ (y\) の向きに分割した長方形上にできる四角柱の体積を加えます。 次に,こうしてできた四角柱の体積の和を \ (x\) 軸の方向に足していきます。 すると, \ ( (91)\) の和が出来上がります。 したがって \ \int\hspace




面積や体積のかけ算の順序 おかしな算数教育 身勝手な主張




小6算数 立体の体積 は公式が大事 勉強方法 考え方を紹介 札幌市 西区 琴似 発寒 塾 学習塾 個別指導塾 マナビバ
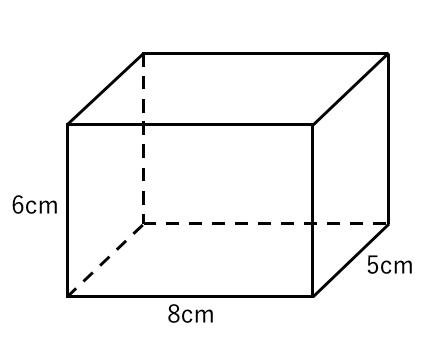
直方体の体積 直方体とは各面が長方形でつくられる図形です。下図に示しました。体積の公式は立方体と同じです。 よって、 直方体の体積=3×4×5=60cm 3 です。 直方体の体積の公式は?1分でわかる求め方、例題、直方体の面積の公式 円柱の体積三角形の計算 横の長さから長方形の面積を公式を使って計算します。 縦の長さaと横の長さbを入力し「長方形の面積を計算」ボタンをクリックすると、縦の長さと横の長さから長方形の面積を計算して表示します。円柱の体積を求める公式は、 V = Sh = πr^2 h で表されます。このページでは、例題と共に、円柱の体積を計算する方法を説明しています。また、斜円柱の体積の求め方も説明しています。
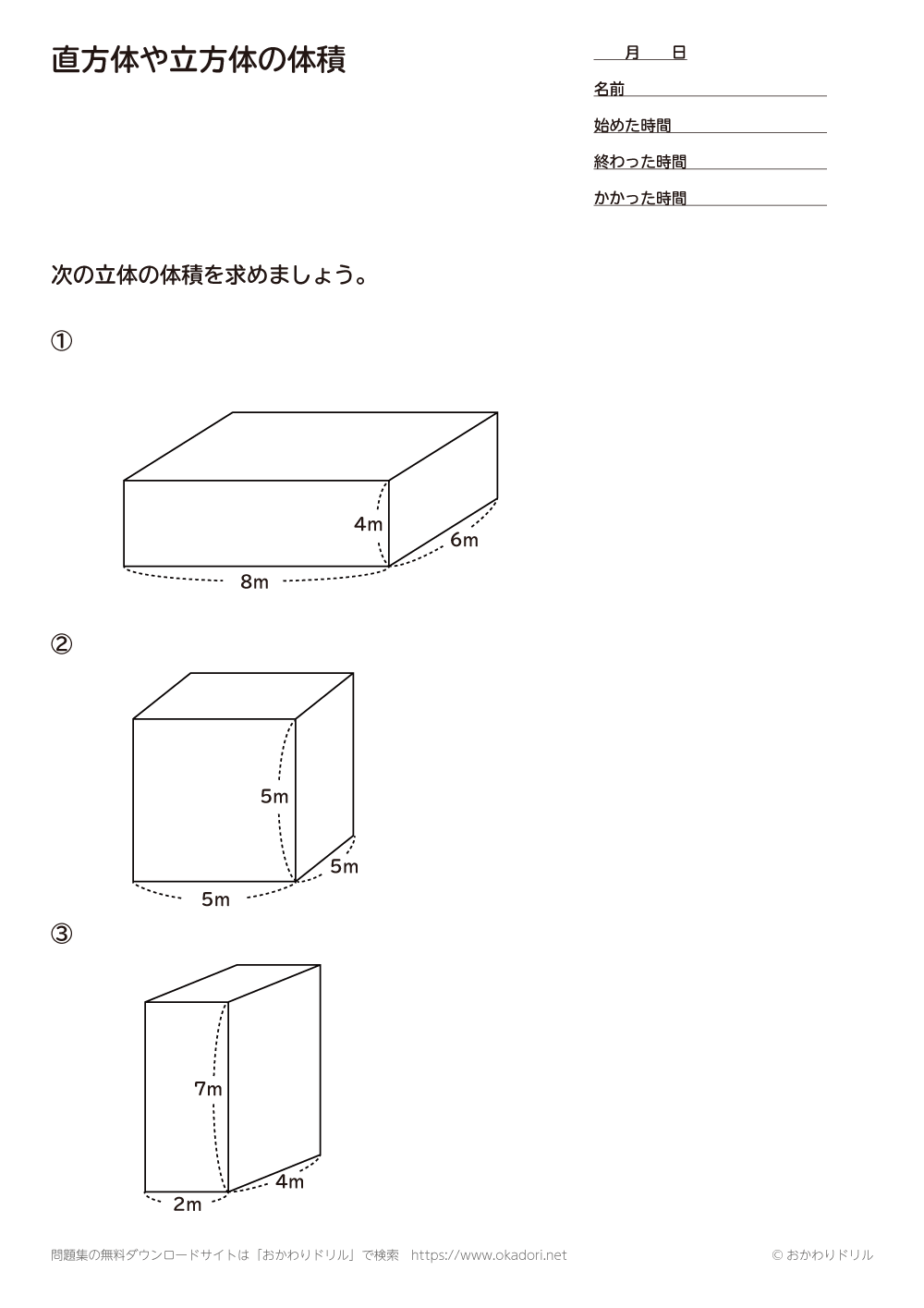



小学5年生 算数 無料問題集 直方体や立方体の体積 おかわりドリル




正方形と長方形は\(1cm^2\)のマスがきちんと整列しているため 『たて×よこ』で面積が求められるというのはきちんと抑えておくのが大事です。 具体的に言うと、 すべての辺が平行ですべての角が直角だから ということです。長方形の面積を求める公式は 長方形の面積 \(=\) たて \(\times\) よこ なので、長方形の面積を \(S\) とすると \ \begin{aligned} S \ &= 6 \times 3 \\ &= 18 \(cm^2) \end{aligned} \ になります。 次はたて・よこの長さが小数点を含む長方形の面積を計算します。 練習問題②・その3_ 大きな面積の単位 4年 大きな面積の単位いろいろ 紙に書いた図形の広さだけなら「cm 2 (平方センチメートル)」だけでじゅうぶん、これ1つでこと足ります でも、公園の広さとか、田んぼの広さ、国の広さなんて大きな広さ(面積)を考えなきゃなりませんね。




5年 直方体と立方体の体積 算数イメージ動画集 大日本図書




計算公式 立方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく
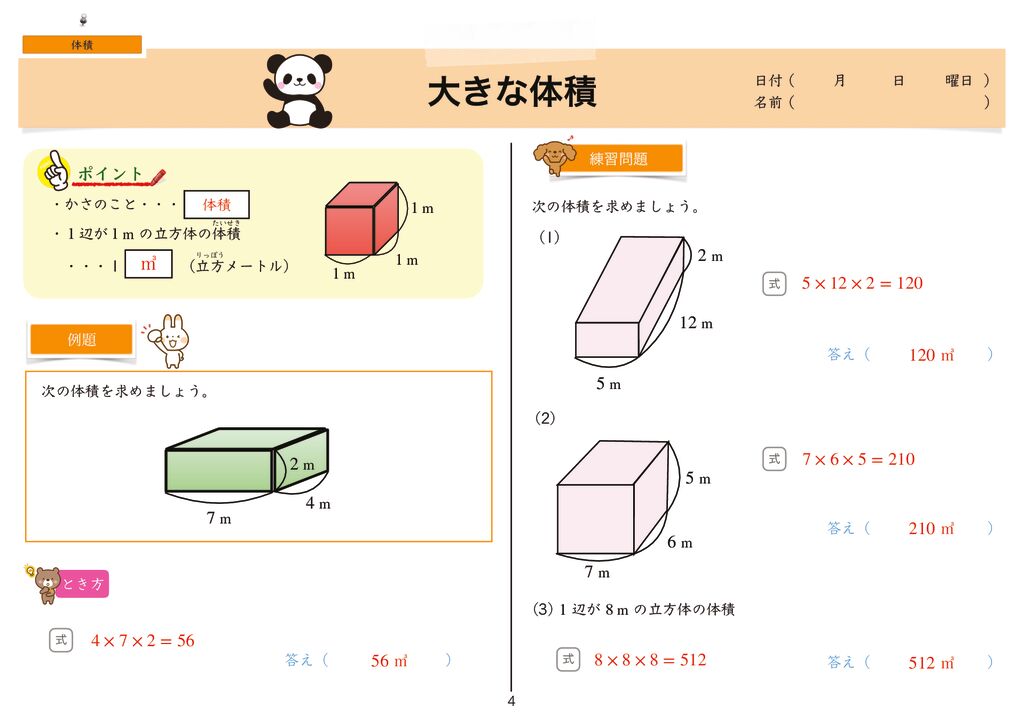



世界一分かりやすい算数 小5 体積



地図の体積計測




直方体 立方体の体積 Youtube



算数科予習プリント 体積の求め方は考えられたかな 翁島 おきなしま 小学校ホームページ




角柱の体積の公式 求め方は底面積と高さに注目するだけだ 中学や高校の数学の計算問題



1
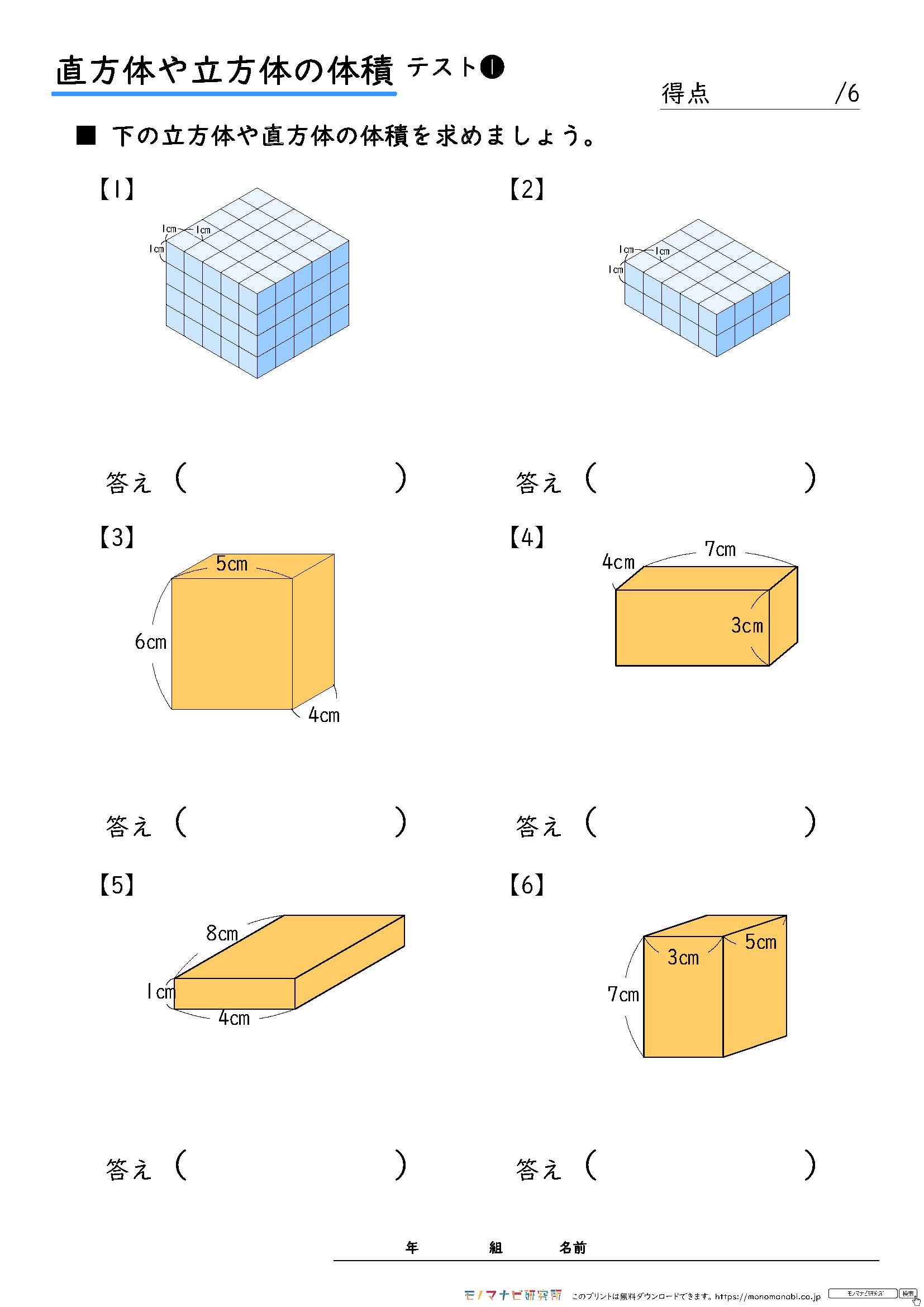



モノマナビ研究所



1



2




中学受験 算数 立体図形の体積の求め方 公式の成り立ちから詳しく解説 中学受験アンサー




微分を使って直方体の容積の最大値を求める方法




計算公式 直方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




四角錐台の体積 高精度計算サイト




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強
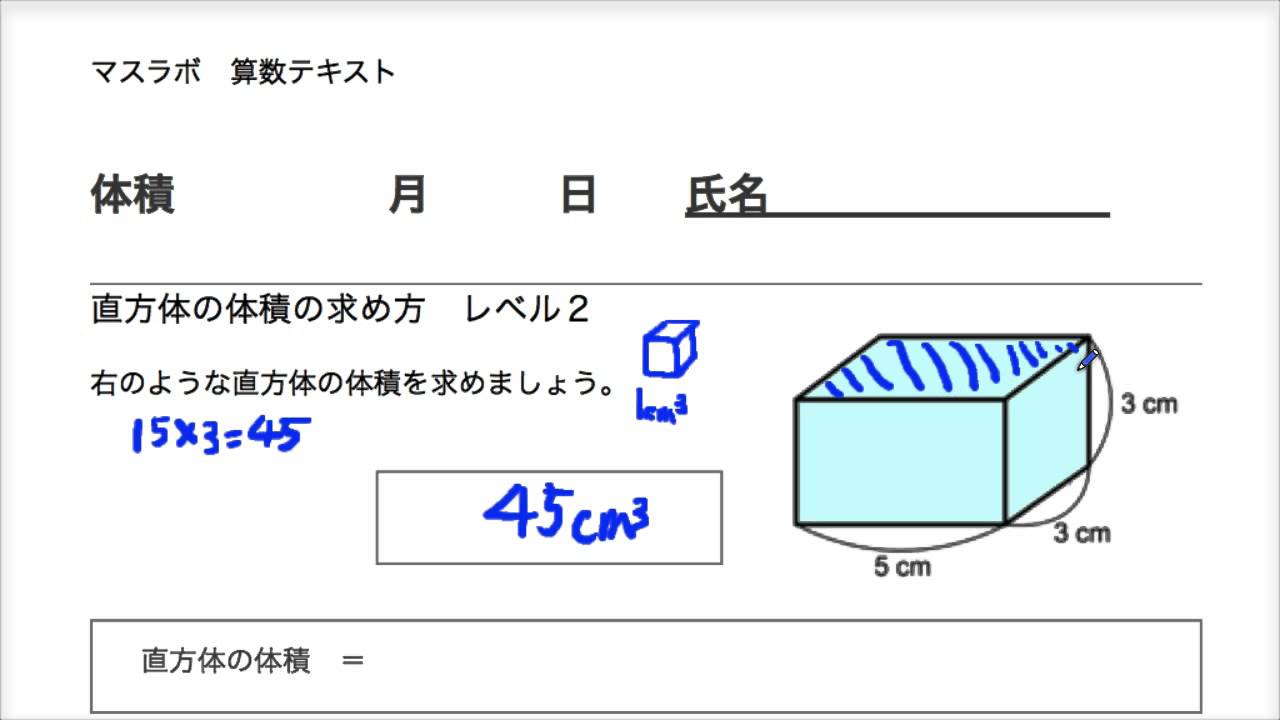



マスラボ 小学校5年 体積 レベル2 直方体の体積の求め方 Youtube
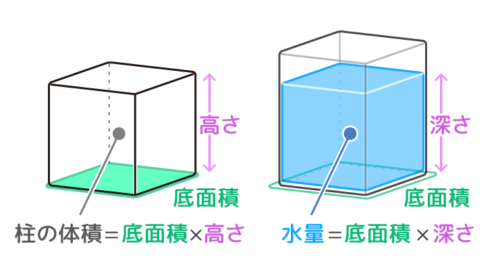



作成中 中学受験 容積 水の問題の解き方は 傾けたり物を沈めたり そうちゃ式 受験算数 2号館 図形 速さ
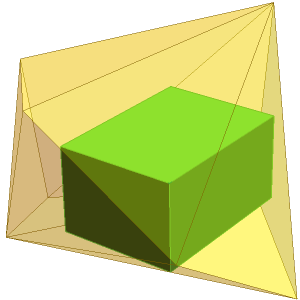



最大体積の直方体 Wolfram言語 12の新機能



5年算数体積2わかる教え方




相似な直方体の表面積比 体積比 中学数学 By Okボーイ マナペディア




11番と12番の解き方を教えて欲しいです Clear




体積の求め方 計算公式一覧




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強
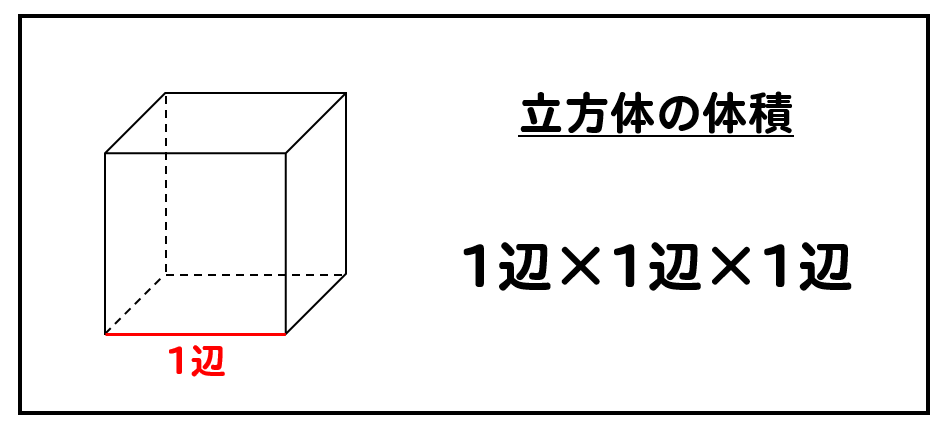



立方体の体積 小学生はどうやって問題解く 計算のやり方を解説 数スタ



算数流体積の求め方 Sciencelab 冨田塾




立体の体積問題 12年 麻布中学校 恋する中高一貫校 適性検査 徹底攻略



1
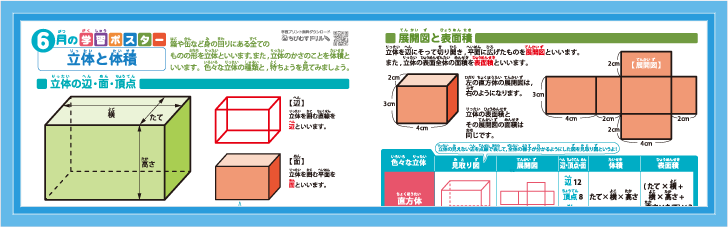



小学算数 立体と体積 直方体 立方体 三角柱 円柱 四角すい 円すい 辺 面 頂点 展開図 体積と表面積の公式 学習ポスター クイズテスト やってみよう ちびむすドリル 小学生学習ポスター テスト 家庭学習シート 3ステップ学習



Www Pref Chiba Lg Jp Kyouiku Shidou Gakuryoku Cc100 Sannsuu Documents S5 023 Pdf
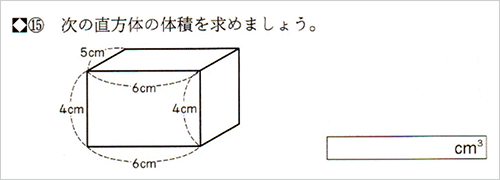



私の実践 私の工夫 算数 直方体や立方体の体積 児童が既習の知識と結び付けて考察できる授業を目指して 啓林館



Www Aen Arakawa Tokyo Jp Higurashi E Action Common Download Main Upload Id 1599




角柱の体積 Youtube
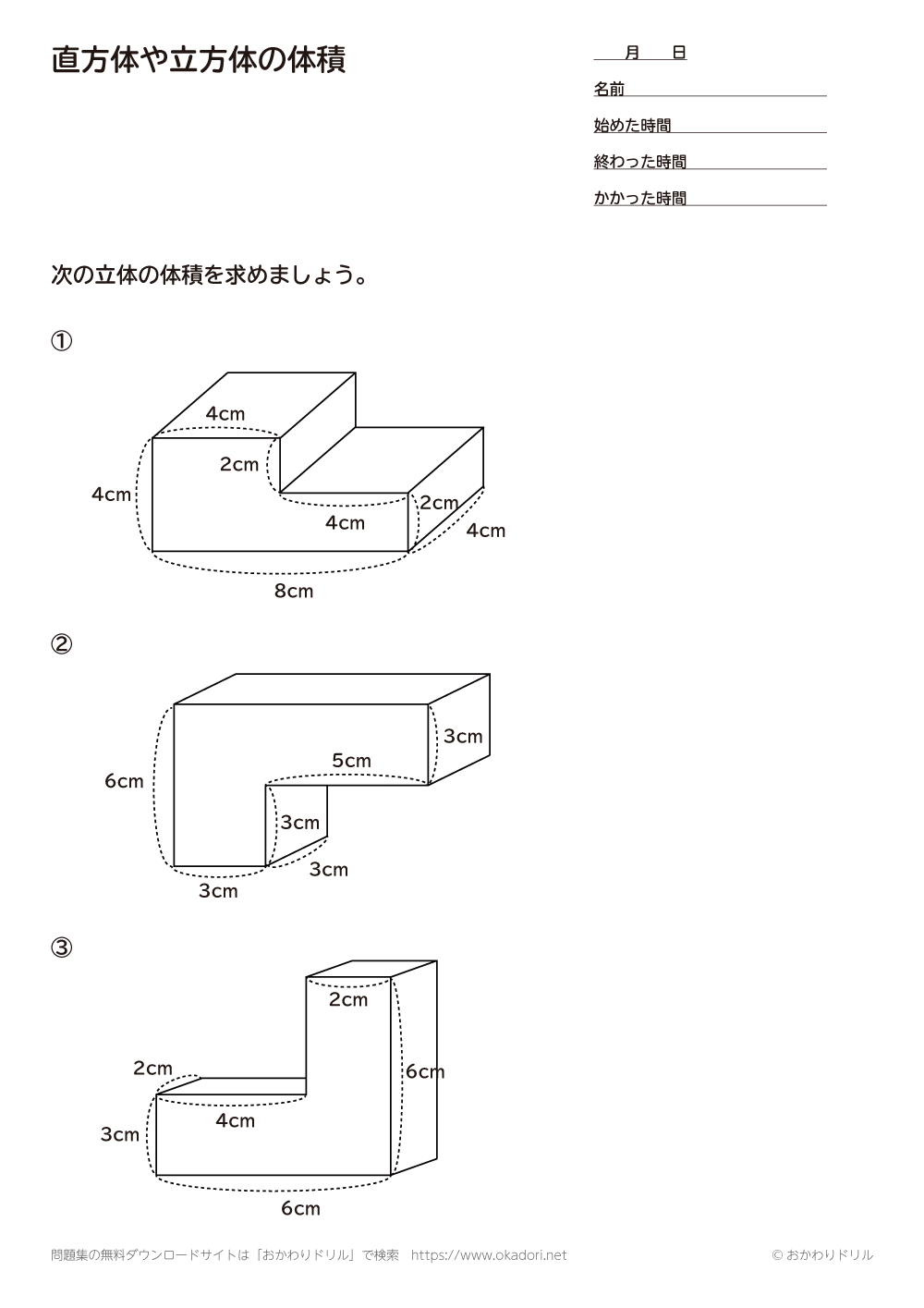



小学5年生 算数 無料問題集 直方体や立方体の体積 おかわりドリル



Www Pref Gunma Jp Contents Pdf




私の実践 私の工夫 算数 直方体や立方体の体積 児童が既習の知識と結び付けて考察できる授業を目指して 啓林館




11 3sqrt3 Cm 36cm Sqrt6 Descubre Como Resolverlo En Qanda




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強




中1数学 三角すい 四角すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット
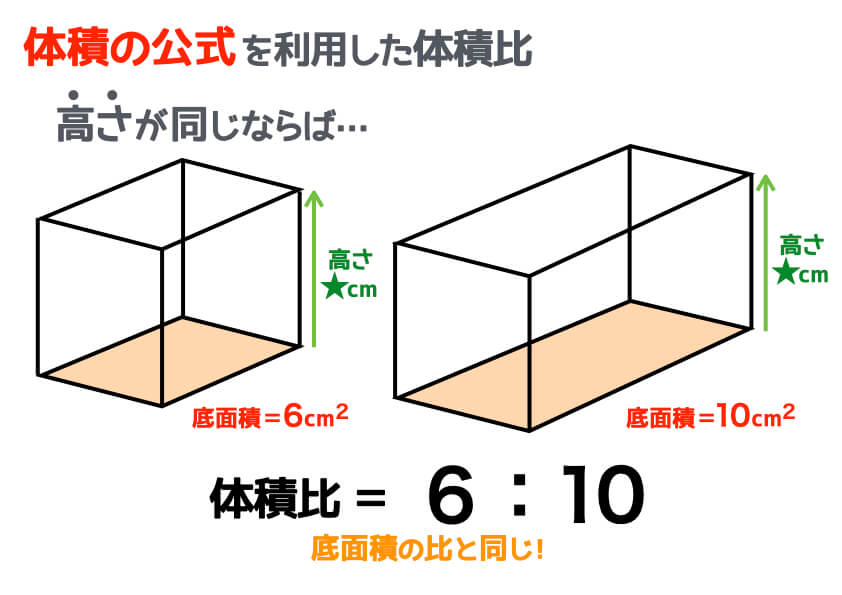



小学生でもスッキリ理解できる 体積比のコツと求め方 中学受験ナビ



立方体の切断と体積 東邦大学付属東邦中学 2017 どう解く 中学受験算数
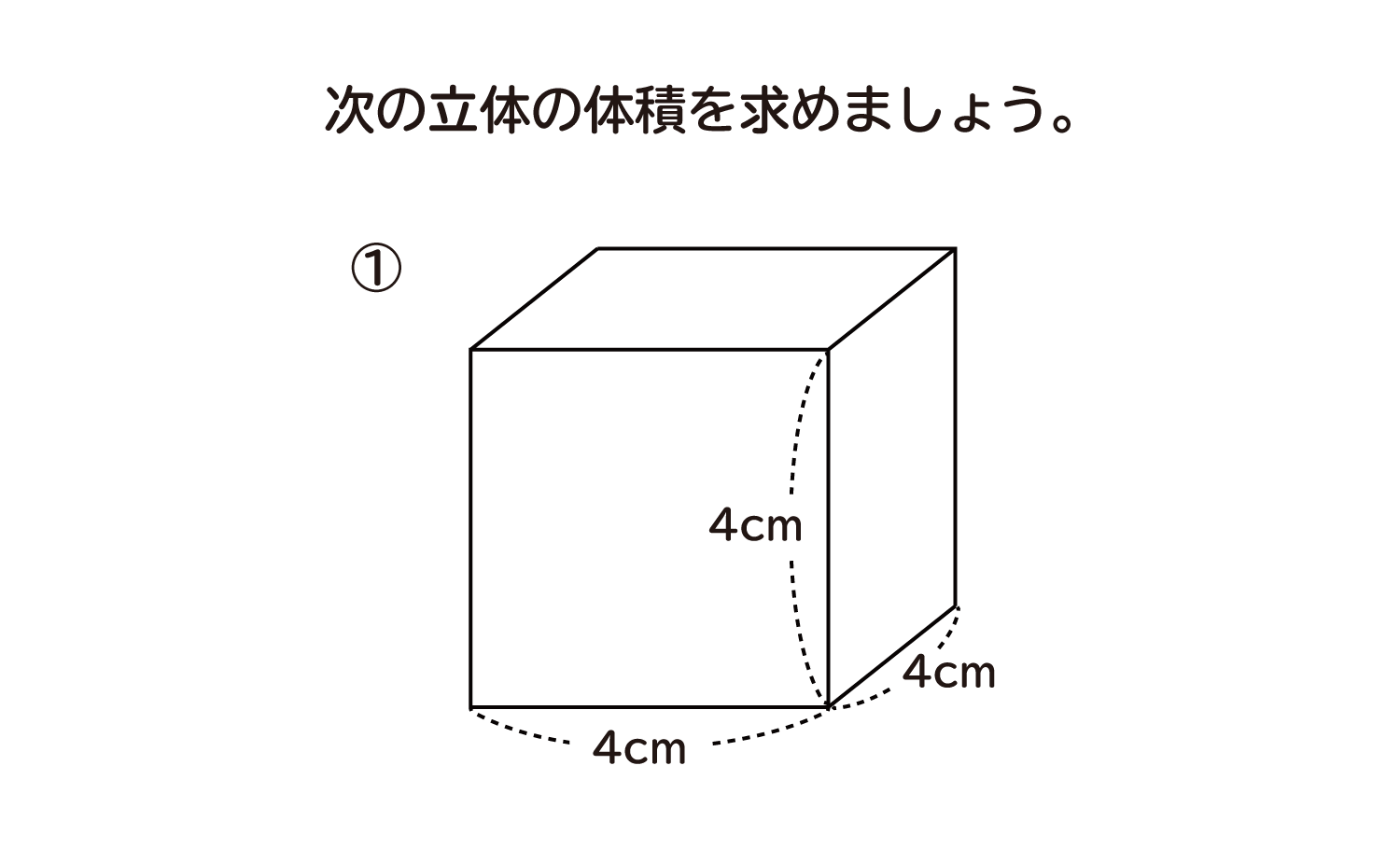



小学5年生 算数 無料問題集 直方体や立方体の体積 おかわりドリル
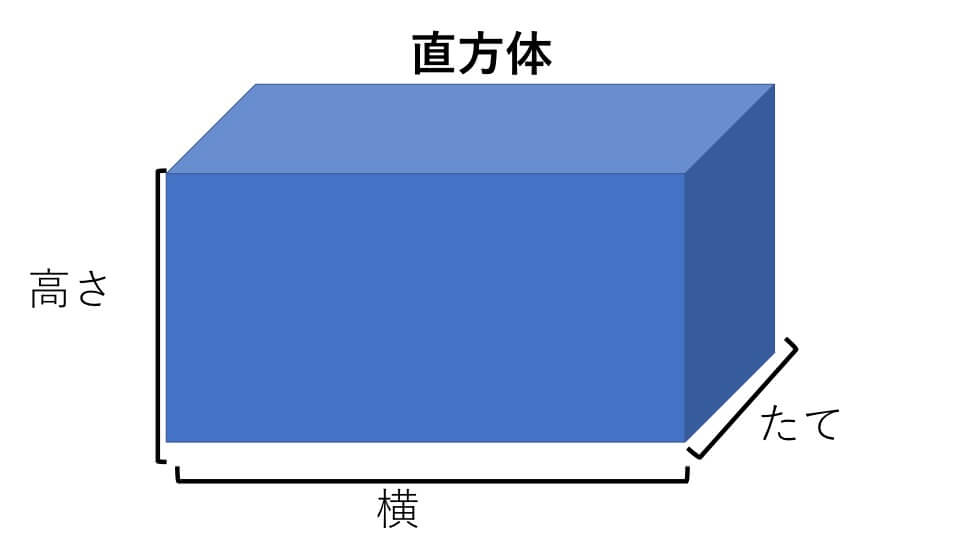



中学受験 算数 立体図形の体積の求め方 公式の成り立ちから詳しく解説 中学受験アンサー




立方体の表面積と体積を求める公式と計算問題 単位との関係も ウルトラフリーダム



Www Nagoya C Ed Jp School Shimizu E 5sansu A Pdf




立体の体積を求める公式




中1数学 立体の表面積と体積の求め方と練習問題 Pikuu



Www Pref Chiba Lg Jp Kyouiku Shidou Gakuryoku Cc100 Sannsuu Documents S5 005 Pdf




円柱 の 求め 方 円柱の体積の求め方 公式 Amp Petmd Com




どうして1 3なの 錐の体積の公式の求め方 まなべーと



Math 容器にものを入れる問題 公式 体積 底面積 高さ の応用 働きアリ



5年算数体積2わかる教え方




10 68m 39m M Descubre Como Resolverlo En Qanda
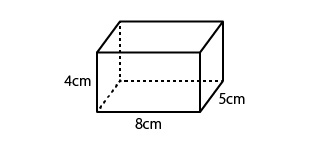



直方体の計算 もう一度やり直しの算数 数学




立方体 直方体の体積の求め方 小学生に教えるための分かりやすい解説 数学fun
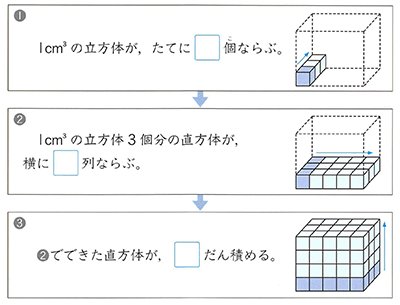



Kistenkasten723 5年生は どうして 直方体の体積が縦 奥行 横 幅 高さという公式で求められるかを学習しています 単元テストは 入試や検定試験などと違い 授業の一環であり 授業でやったことができるかどうかを確認するのが目的です




体積の求め方 計算公式一覧
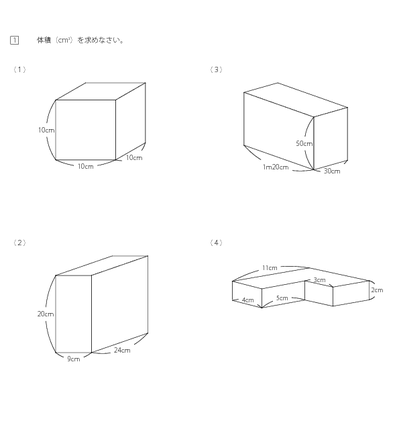



みんなの算数オンライン 教科書 立方体 直方体の体積と単位




算数 新 小5編 体積 小4から始める高校受験 お母さん 一緒にがんばりましょう




小学5年生の算数 体積 直方体と立方体を組み合わせた立体の体積を求める問題 ちびむすドリル 小学生




計算公式 直方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく
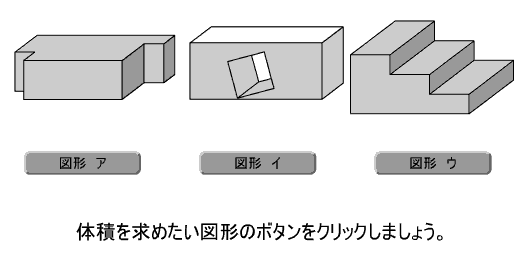



算数科5年 体積 導入 発展教材ソフトを使った授業 Note Board



Www Kyoiku Metro Tokyo Lg Jp School Study Material Improvement Tokyo Basic Drill Files Math Pr05 5nen 10a Pdf
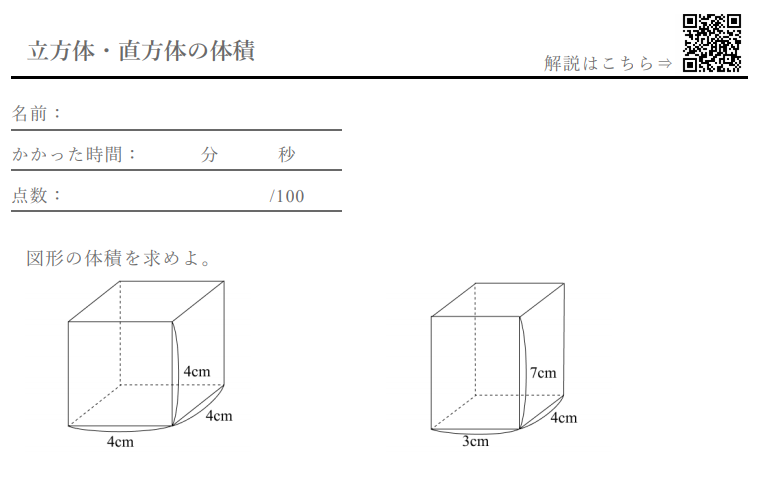



立方体 直方体 の体積 計算ドリル 問題集 数学fun



直方体 立方体の体積 On Vimeo



立方体の体積 簡単に計算できる電卓サイト



6年算数立体の体積1 教え方
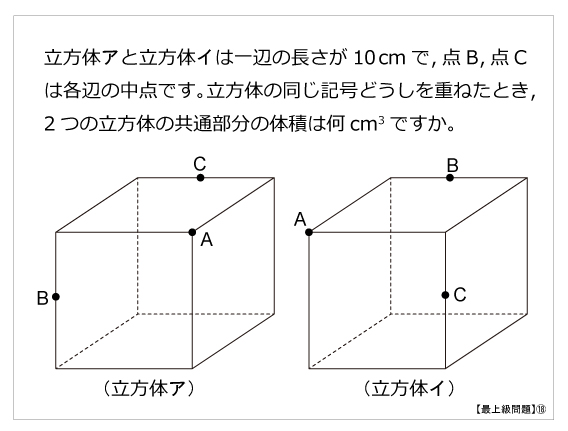



最上級問題 立方体の共通部分 算数星人のweb問題集 中学受験算数の問題に挑戦



1



Http Www Edu Tens Net Syohp Murehp Kyuukou Purinto Pridata 5nen 5san2 Pdf




立方体を対角線まわりに1回転させてできる回転体の体積 数学の偏差値を上げて合格を目指す



図形noteプレ レベル4 直方体の体積 算数星人のweb問題集 中学受験算数の問題に挑戦



動画で学習 体積 その2 算数




体積 複雑な形の立体 算数 教科質問ひろば 進研ゼミ小学講座
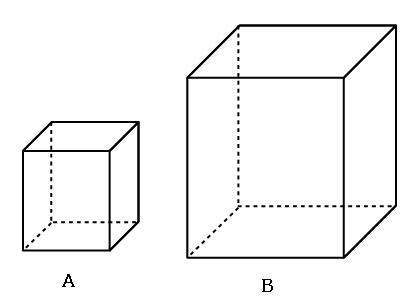



相似比と面積比と体積比の関係を解説 公式を使って面積や体積を求めよう




三角柱の体積 表面積の求め方が図で誰でも即わかる 展開図も紹介 高校生向け受験応援メディア 受験のミカタ



立体の体積 困難 直接求められない体積 は 分解せよ たすか ひくか 立方体 正六面体 を4回切ってできる正四面体の体積 は 立方体の3分の1 ワンセンテンス算数 Note
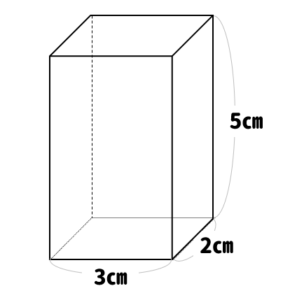



3分でなるほど 四角柱の体積 表面積の求め方をマスターしよう 数スタ




体積の求め方 計算公式一覧
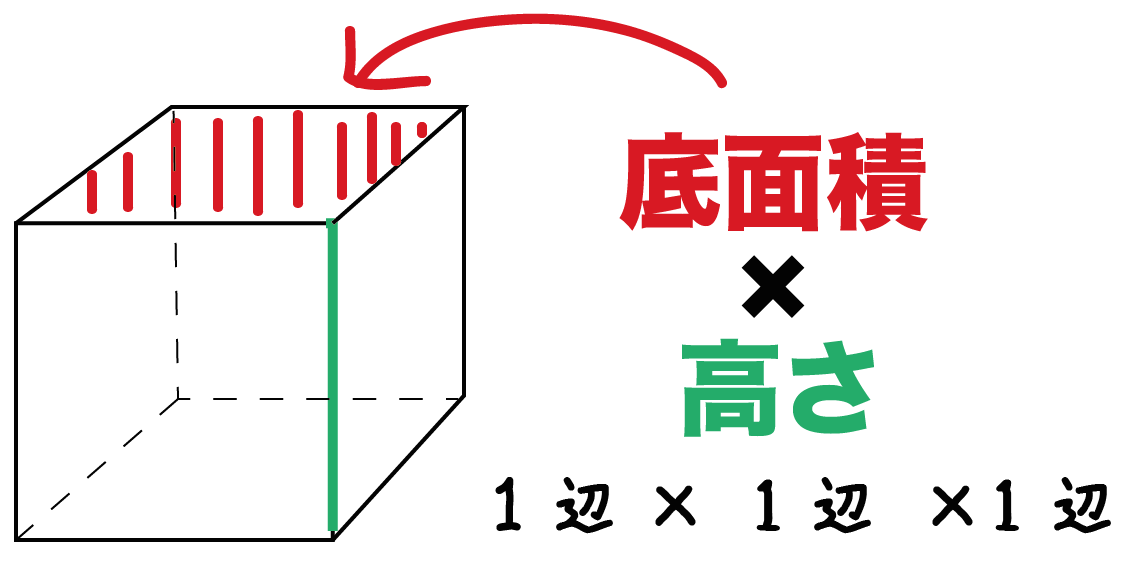



計算公式 立方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく



Http Nk Minamidai E La Coocan Jp Kadai 5nen R0525 5nen Math03 1 2 Pdf
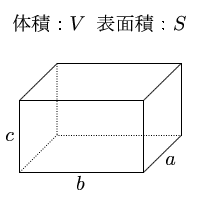



直方体の体積 表面積 体積 表面積の計算 計算サイト




すきるまドリル 小学5年生 算数 体積 無料学習プリント すきるまドリル 無料学習プリント




計算公式 立方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく
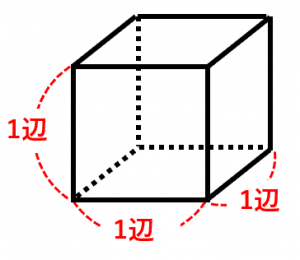



立方体と直方体の体積を計算する方法とツール 具体例で学ぶ数学




表面積一定の円柱と直方体の体積の最大値 理系のための備忘録
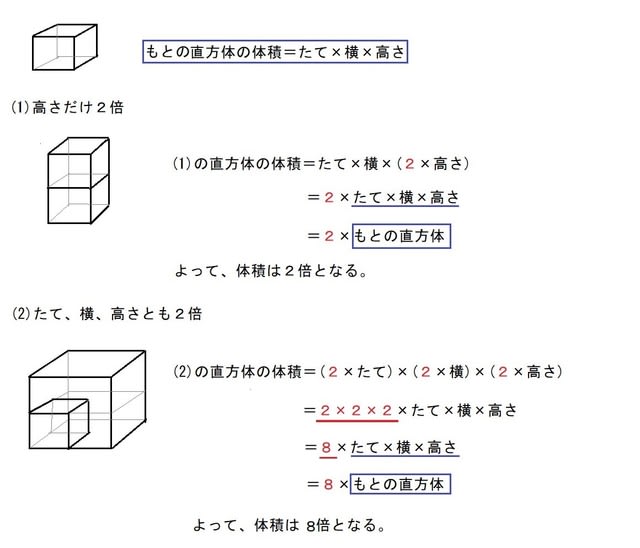



直方体 立方体の体積 小5 きちんと式を書けば簡単 算数の教え方教えますmother S Math Happy Study Support



立方体の公式は 1分でわかる意味 体積の公式と例題の求め方 表面積の公式
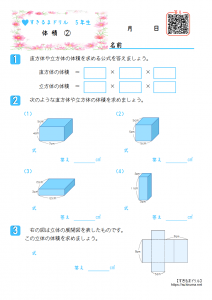



すきるまドリル 小学5年生 算数 体積 無料学習プリント すきるまドリル 無料学習プリント
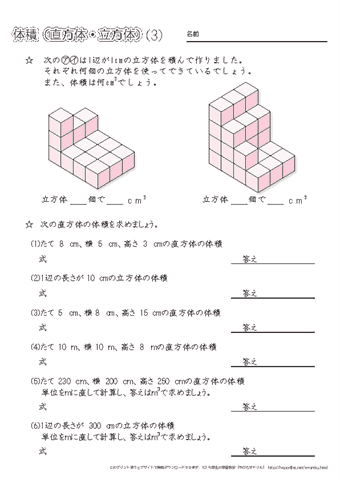



小学5年生の算数 体積 直方体と立方体の体積の求め方 練習プリント ちびむすドリル 小学生




小5 算数 小5 3 直方体と立方体の体積 Youtube
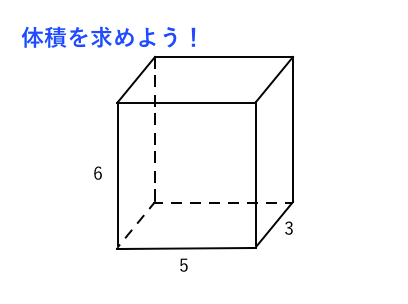



超簡単 体積の求め方 苦手な数学を簡単に


